Определение прогиба балки в середине пролета

Ход выполнения расчета

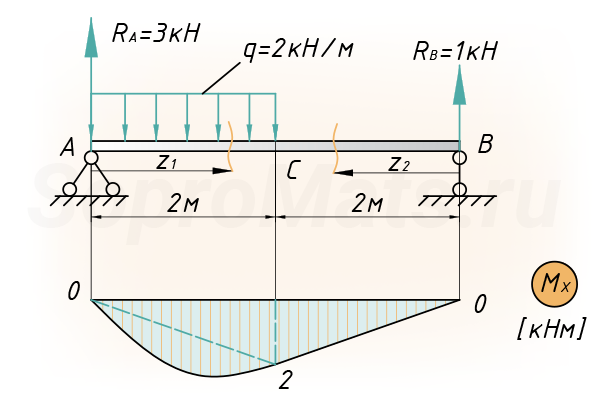
Сначала строим эпюру изгибающих моментов, для рассчитываемой балки:

Расслаиваем эпюру на простейшие фигуры:

Построение единичной эпюры

Прикладываем единичное усилие по направлению искомого перемещения (в точке С) и строим от этой силы эпюры моментов:

Вычисление прогиба

Вычисляем прогиб сечения C по методу Мора — Верещагина (слева направо):

\[ { V }_{ C }=\frac { 1 }{ E{ I }_{ x } } (\frac { q{ \cdot 2 }^{ 3 } }{ 12 } \cdot \frac { 1 }{ 2 } \cdot 1+\frac { 1 }{ 2 } \cdot 2\cdot 2\cdot \frac { 2 }{ 3 } \cdot 1+\frac { 1 }{ 2 } \cdot 2\cdot 2\cdot \frac { 2 }{ 3 } \cdot 1)=\frac { 10кН{ м }^{ 3 } }{ 3E{ I }_{ x } } \]

По сортаменту двутавров выписываем значение момента инерции балки и вычисляем численное значение прогиба:

\[ { I }_{ x }=350{ см }^{ 4 } \]

\[ { V }_{ C }=\frac { 10кН{ м }^{ 3 } }{ 3E{ I }_{ x } } =\frac { 10\cdot { 10 }^{ 9 }Н\cdot { см }^{ 3 } }{ 3\cdot 2\cdot { 10 }^{ 7 }\frac { Н }{ { см }^{ 2 } } \cdot 350{ см }^{ 4 } } =0.476см \]